| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- algorithm
- node.js
- 개발공부
- REACT
- JavaScript
- 자바스크립트
- Python
- 자료구조
- Zerobase
- 자바
- execution context
- 글또
- 컴퓨터공학
- java
- 파이썬 알고리즘 인터뷰
- 코드스테이츠
- 알고리즘
- react 기초
- Computer Science
- 비동기
- python algorithm
- 운영체제
- OS
- useState
- 파이썬
- 테스트코드
- 프로그래머스
- context switching
- Operating System
- codestates
- Today
- Total
Back to the Basics
[Algorithm] - 제곱근 , 소수점 구하기 본문
기초 알고리즘 문제를 푸는 도중 제곱근의 수를 입력받아 제곱근 값을 소수점 2번째 자리까지 구하는 문제가 나왔다.
Math.sqrt라는 아주 좋은 메소드가 있지만, 사용하면 안 된다고 한다.
이 문제에서 구현해야 햘 기능을 나눠보면, 1) 제곱근을 구하고 2) 소수점 2번째 자리까지 출력이라고 할 수 있다.
문제는 금방 풀었지만, 고등학교 수학인가 중학교 수학인가 에서 배웠던 수학적인 방법들이 생각나서 추가적으로 구현해 보았다.
그리고, 문제에서 힌트로 주어져있던 바빌로니아 알고리즘에 대해서도 마지막
첫 번째 풀이
학창시절 배우고, 공업수학도 대학에서 해서 그런지 이 정도는 아직.. 아직 기억이 난다..ㅋㅋㅋ..
제곱근은 루트 안에 숫자를 넣은 값이다. 이를 계승으로 표기하면 숫자^(1/2) 승이다. 3세곱근은 숫자^(1/3)이고..
그래서 첫 번째 기능인 "(1) 제곱은 구하기"는 쉽게 구할 수 있었다.
(2) 소수점 2번째 자리를 구하는 방법은 제곱근을 쉽게 구했기에 간단하게 구할 수 있었다.
수도 코드를 먼저 작성해보면 아래와 같다.
// 힌트를 사용하지 않고 직접 구해본다.
// let sqrt 제곱근을 0.5승 을 하여 구한다.
// 소수점을 구하기 위해 아래의 단계를 시행한다
// 1. num1 num2 를 각각 선언하고 num1=pareInt(sqrt*1000)을 num2=parseInt(sqrt*100)*10을 해준다.
// 2. num3을 선언하고 num1-num2의 결과를 넣고
//결과를 넣을 result 변수를 선언한다
// 3. 만약 num3이 5보다 크거나 같으면, result=num2+10을 할단한다.
// 4. 작다면, result=num2를 할당한다.
// result*10**(-3)을 출력한다.
두 개의 변수를 선언하고, 한 개의 변수엔 셋째 자리수까지의 값이, 두 번째 변수엔 3째 자릿수이지만 마지막에 0이 되게 만들었다.
두 변수의 차이가 5 이상이면 반올림을 해야 하므로, 두 번째 변수에 10을 더하여 둘째 자릿수를 올려준다.
5 미만이면, 3번째 자리수를 버린 두 변째 변수를 그대로 결과로 받는다.
코드로 옮기면 아래와 같다.
// 제곱근을 구하는 방법 1
let sqrt=num**0.5;
// 소수점 2번째 자리까지 구하는 방법 1.
let num1=parseInt(sqrt*1000);
let num2=parseInt(sqrt*100)*10;
let num3=num1-num2;
let result=0;
if(num3>=5)result=num2+10;
else result=num2;
return result*10**(-3);
}두 번째 풀이
- 근삿값을 구하면 소수 두 번째 자리까지 구하는 방법은 위의 방법처럼 구할 수도 있고, Number의 Metho를 사용하여 구할 수 있다.
// 소수점 몇 번째 자리까지 구하는 방법 2 : toFixed 를 사용한다.
function financial(x) {
return Number.parseFloat(x).toFixed(2);
}- 근사값을 구하는 두 번째 방법은, 고등? 중학교 수학에서 루트의 근사값을 구할 때 배웠던 방법을 활용하였다.
a < sqrt(number) < b의 범위라고 했을 때, 범위를 계속 좁혀가는 방식으로 구한다.
a와 b의 평균값인 (a+b)/2를 근삿값이라고 가정을 하고, 제곱함 값이 number보다 큰지, 작은지 비교한다.
만약 Number보다 작으면 이 평균값을 a로, 크면 b로 재할당 하면서 number의 범위를 좁혀나간다.
수도 코드는 아래와 같다.
// a< sqrt(num) <b 에서
// a =1
// b의 초기값을 구하는 구문
// 반복문을 사용하여 b의 초기값을 구한다
// while(true) b+=1 b*b>num -> break
// sqrt(x)의 근사값을 구하는 방법은 a< x <b 일 때,
//if b-a<=0.01 x=a,break 일때까지 반복문을 돌린다
// (a+b/2)^2 > x ==> b==> a+b/2
// (a+b/2)^2 < x ==> a==> a+b/2위의 방법은 반복문을 사용해야 해서 1번 방법보다는 비효율적인 방법이긴 한 것 같다.
구현한 코드는 아래와 간다.
// 1. a,b 초기값 구하기
let a=1,b=0;
// let num=3;
while(true){
b+=1;
if(b*b>num) break;
}
// 2. num의 근사값 구하기
let sqrt=0;
let temp=0; // 제곱하여 num과 대소 교를 할 값을 넣은 임시변수
while(true){
if((b-a)<=0.001){
sqrt=a
break;
}
temp=(b+a)/2;
if(temp**2>num) b=temp;
else a=temp;
}
console.log(sqrt);
} 바빌로니아 알고리즘
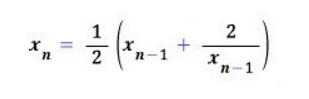
바빌로니아 알고리즘은 5-6여 년 전 수학 기호는 없었지만, 그들이 사용했던 방법이라고 한다. 대단하닿..
먼저 수식을 보면 아래와 같다.
$x_{n+1} = \frac{1}{2}(\frac{number}{x_{n}} + x_{n})$ 으로 표현할 수 있다.
$\lim_{n\to \infty}x_{n}$를 구하면 된다.
이 방법은 위의 범위를 좁혀가는 방식과 비슷한 방식인 것 같다. 풀이를 하면, 아래와 같다.
Num의 근삿값을 구하려고 하고, $ x_{n} < \sqrt{Num} $ 이라고 가정한다.
$ \frac{1}{x_{n}} > \frac{1}{\sqrt{Num}} $
$ \frac{1}{x_{n}} > \frac{\sqrt{Num}}{Num} $
$ \frac{Num}{x_{n}} > \sqrt{Num} $
이과 같이 Num의 범위를 아래와 같이 구할 수 있다.
$ x_{n} < \sqrt{Num} < \frac{Num}{x_{n}}$
이제, 두 범위의 평균값을 구하고 그 값을 $x_{n+1}$ 이라 한다.
$ x_{n+1}= \frac{x_{n} + \frac{Num}{x_{n}}}{2}$
$ x_{n+1}= \frac{1}{2}(x_{n} + \frac{Num}{x_{n}})$
이제, 일반항을 구했으니 극한으로 보내주면 답이 나온다..!
수학을 다른 과목보다 좋아하는 편이었는데, 특히 주관식 문제에서 문제를 읽고 문제의 일반식을 유도하여 구하는 문제를 좋아했는데 굉장히 비슷한 방식이다.
다시 이렇게 오랜만에 수식을 고민하고 직접 구해보니 재밌었다.
코드로 구현하는 건 내일 해보고 추가해야겠다.
'Computer Science > Algorithm & Data Structure' 카테고리의 다른 글
| [자료구조/알고리즘][Codestates] Stack (0) | 2021.09.20 |
|---|---|
| [자료구조/알고리즘]재귀 - JSON - Serialize & Deserialize (0) | 2021.09.10 |
| [Programmers-python algorithm] - 5강 (0) | 2021.07.04 |
| [Programmers-python algorithm] - 4강 (0) | 2021.07.03 |
| [Programmers-python algorithm] - 3강 (0) | 2021.07.03 |


